El conocidísimo cubo de Rubik:
quizá sea uno de los más populares ejemplos de un objeto detrás del cual los conceptos de simetría están operando directamente.
Creado en 1974 por Erno Rubik, un escultor y profesor de arquitectura húngaro, el cubo de Rubik saltó a la fama en 1980 cuando la locura del cubo atrapó a muchos entusiastas alrededor del mundo, y el cual para 1982 había sido vendido en más de 100 millones de cubos, convirtiéndose en uno de los juguetes más vendidos de todos los tiempos. Sin embargo, pese a que ha estado con nosotros por más de tres décadas, y pese a los enormes avances que ha habido en los campos de las ciencias computacionales y las matemáticas, el cubo de Rubik aún guarda muchos secretos. Apenas en el mes de julio de 2007 los científicos en ciencias computacionales Dan Kunkle y Geene Cooperman lograron probar que cualquier configuración posible del cubo de Rubik puede ser resuelta en 26 pasos, auxiliados para su descubrimiento por una supercomputadora pero también por matemática astuta, lo cual fue indispensable considerando que hay
o bien:
43,000,000,000,000,000,000
diferentes configuraciones posibles. Los detalles de la solución lograda por ellos está reportada en el siguiente enlace:
http://www.ccs.neu.edu/home/gene/papers/rubik.pdf
Sin embargo, esto no es el fin del asunto, ya que un gran número de matemáticos expertos cree que cualquier configuración posible del cubo de Rubik puede ser resuelta con un máximo de 20 movidas (lo cual está apoyado por el hecho de que los campeones humanos en la resolución del cubo de Rubik rara vez necesitan más de 20 movimientos para restaurar un cubo de Rubik a su configuración original, un hecho confirmado en la competencia internacional convocada por la World Cube Association llevada a cabo en España en mayo de 2007 en donde el récord mundial para la resolución de un cubo totalmente desconfigurado fué cronometrada en 9.86 segundos). En realidad, nadie sabe exactamente cuál es el número mínimo de movimientos que se necesitan para volver a reconfigurar cualquier cubo de Rubik, este es un número del que se dice que “sólo Dios lo sabe”, razón por la cual algunos expertos en teoría de grupos lo llaman “el número de Dios” (es interesante ver cómo hasta la teología puede pasar a formar parte de las matemáticas de la simetría).
No entraré en detalles aquí sobre la manera de restaurar un cubo de Rubik a su configuración original, ya que hay numerosos sitios en Internet en donde se dan liberalmente muchos algoritmos (procedimientos de solución) para lograr la restauración del cubo de Rubik, e inclusive hay proramas gratuitos procurables de Internet que pueden correr bajo prácticamente cualquier computadora de escritorio los cuales pueden darle a una persona un procedimiento de solución paso-a-paso para su cubo de Rubik. Uno de dichos programas para ser corrido bajo Windows, Rubik.exe, el cual se distribuye gratuitamente en el siguiente enlace:
http://www.geometer.org/rubik
presenta la siguiente interfaz:
La documentación para utilizar este programa gratuito de solución se puede descargar del enlace:
www.geometer.org/rubik/group.pdf
Hay varias versiones del cubo de Rubik que van desde una más elemental, el "cubo de Rubik 2x2x2" (conocida también como "Rubik's Junior"):
pasando por el "cubo de Rubik 4x4x4" (conocido como "la venganza de Rubik):
hasta llegar al "cubo de Rubik 5x5x5" (conocido como el "Rubik Professor):
así como cubos asimétricos tales como el "cubo de Rubik 2x2x3":
y el "cubo de Rubik 3x3x4":
además de otras variantes exoticas como la "bola Rubik" (la cual en realidad es un cubo de Rubik 3x3x3 deformado topológicamente para tener el aspecto de una esfera, conservando todas las propiedades del grupo original, con lo cual cualquier persona que sepa reconfigurar un cubo Rubik a su estado original podrá reconfigurar también sin problema alguno una bola Rubik a su estado original):
y la pirámide "Pyraminx" inventada en forma independiente (y antes de que Rubik inventara su cubo) por Uwe Mèffert:
cuyas rotaciones posibles se muestran a continuación:
así como el "Skewb" (adaptado de la palabra inglesa "skewed" que significa "ladeado", al estilo "Rubik"), también inventado por Uwe Mèffert:
o el "Diamante Skweb" (un octaedro regular de 8 caras), también inventado por Uwe Mèffert:
así como el “Megaminx”, un dodecaedro regular de 12 caras (no se asuste nadie, pese a su aspecto aquí no hay ningún “grupo” satánico involucrado detrás del diseño o la construcción de este juguete):
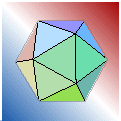
hasta llegar al que tal vez sea el más interesante de todos, el Dogic, el cual es un icosaedro cuyo grupo de permutación S5 es precisamente la razón por la cual una ecuación general de quinto grado no es soluble por radicales:
El lector observador tal vez se haya dado cuenta ya de que este objeto es, geométricamente hablando, el mismo que el que se ha usado al principio como ícono introductorio a todos los capítulos de los que consta esta obra.
Resolvedor del cubo de Rubik (applet Java):
http://www.megasolver.com/html/Java3D/FAQ_EN.htm
"cristal Pyraminx":
No todas las combinaciones que podamos imaginar sobre el cubo de Rubik son posibles. Se puede demostrar formalmente que partiendo de un cubo en su estado original es imposible obtener la siguiente configuración:
Y así como esta, hay muchas otras. De cualquier modo, existen también muchas configuraciones interesantes, las cuales sí son alcanzables a partir de la configuración original:
http://www.math.ucf.edu/~reid/Rubik/patterns.html
La solución de un cubo de Rubik 3x3x3, definida como restaurar cualquier cubo a su configuración original en la cual las seis caras tienen cada una de ellas el mismo color, es enormemente simplificada por el hecho de que el bloque central en cada cara no puede cambiar de posición. Con solo ver cada bloque central, sabemos de inmediato cuál era el orden original de los colores de un cubo, el orden al cual debe ser restaurado.
Existe una notación convencional, universalmente reconocida, para describir las operaciones llevadas a cabo con un cubo de Rubik 3x3x3. En contra de lo que pudiera creerse, esta notación no está basada en los colores de las caras de un cubo en su configuración original, ya que aunque todo cubo de Rubik requiere de seis colores diferentes para cada una de las caras, la distribución de los colores no sigue regla alguna, depende de cada fabricante aún suponiendo que se usen los mismos colores. Es por ello que para trabajar con una notación sobre un cubo nos basamos en la orientación del mismo usando la siguiente convención de literales para describir cada una de las caras del cubo según lo estamos viendo al tenerlo en nuestras manos:
U ==> Up. La cara superior del cubo.Ahora bien, estas mismas letras se utilizan para denotar las rotaciones dadas a cada cara del cubo. Una letra sencilla indica una rotación de 90 grados en sentido de las manecillas del reloj de la cara a la cual hace referencia. Así, la letra U sola indica que la cara superior del cubo se ha de girar 90 grados en sentido de las manecillas del reloj, mientras que la letra R sola indica que la cara que estamos viendo hacia la derecha se ha de girar 90 grados hacia la derecha.
F ==> Front. La cara frontal del cubo.
B ==> Back. La cara trasera del cubo.
R ==> Right. La cara derecha del cubo.
L ==> Left. La cara izquierda del cubo.
D ==> Down. La cara inferior del cubo
Para indicar una operación inversa, en sentido contrario a las manecillas del reloj, utilizamos un superscrito de -1 tal y como se acostumbra en el lenguaje de la simetría. Así, la letra sencilla U-1 indica una rotación de 90 grados de la cara superior del cubo en sentido contrario de las manecillas del reloj.
Pero en lo que realmente estamos interesados es en secuencias de operaciones, esas secuencias de operaciones que “descomponen” al cubo. Se ha adoptado la convención de que una secuencia de operaciones sea listada de izquierda a derecha, tal y como lo hemos venido haciendo en nuestro lenguaje de la simetría al llevar a cabo operaciones binarias. De este modo, la secuencia:
F ○ U
abreviada simplemente como la secuencia FU, nos dice "girar la cara frontal del cubo 90 grados en sentido de las manecillas del reloj, y tras esto girar la cara superior del cubo 90 grados en sentido de las manecillas del reloj".
Del mismo modo, una secuencia más elaborada de operaciones sobre el cubo de Rubik:
F ○ U ○ R-1 ○ F-1 ○ U ○ F-1
abreviada simplemente como:
FUR-1F-1UF-1
nos va diciendo “empezar aplicando a la cara frontal del cubo una rotación de 90 grados en sentido de las manecillas del reloj, y tras esto aplicar una rotación de 90 grados en sentido de las manecillas del reloj a la cara superior, tras lo cual se aplica una rotación de 90 grados en sentido contrario a las manecillas del reloj a la cara derecha, etc.”
Esta convención nos permite ir anotando en orden todas las operaciones que le vayamos aplicando a un cubo que tengamos en nuestras manos, y además de permitirnos tener un registro de lo que hemos hecho, nos permite reconstituír fácilmente el cubo a su condición original porque todo lo que tenemos que hacer es aplicar la misma secuencia de operaciones en orden inverso.
El cubo de Rubik, aparte del entretenimiento de cientos de horas que puede proporcionar a los adictos a este tipo de pasatiempo y el enorme valor educativo que tiene para ayudar al individuo a desarrollar una intuición tri-dimensional proporcionándole al mismo tiempo una enorme confianza sobre muchos tópicos de la teoría de grupos que anteriormente parecían cosas demasiado abstractas sin aplicación alguna, tiene una razón por la cual se le ha incluído aquí, y ésta es su capacidad para ayudar a entender la naturaleza real de los procesos conjugados. Cualquier secuencia de tres procesos X, Y y Z en donde el último proceso sea el inverso del primero proceso, o sea Z=X-1, es conocido como un proceso conjugado. Precisamente una de las cosas que pueden suscitar muchas dudas a los novatos en la teoría de grupos es la siguiente operación conjugada:
g ○ P ○ g-1
o lo que es lo mismo:
g-1 ○ P ○ g
A primera vista, este proceso conjugado puede despertar la idea de que su único efecto real es llevar a cabo la operación P; porque si se efectúa la operación g y tras esto se efectúa la operación P y tras esto se efectúa la operación g-1 (que es el inverso de g), entonces tomando en cuenta que:
g ○ g-1 = g-1 ○ g = I
ingenuamente se puede suponer que lo único que se ha hecho es deshacer el efecto de la operación g con su inverso g-1, dejando a P como la única operación efectiva, o sea:
g ○ P ○ g-1 = g-1 ○ P ○ g = P
Sin embargo, esto no es así. Cualquiera que tenga duda de esto, todo lo que tiene que hacer es tomar un cubo de Rubik en su configuración original, y aplicar una operación conjugada tal como:
U ○ F ○ U-1
la cual consiste en girar la cara superior 90 grados en sentido de las manecillas del reloj (con la operación U), seguida por un giro de 90 grados en sentido de las manecillas del reloj de la cara frontal (con la operación F) seguida por un giro de 90 grados en sentido contrario de las manecillas del reloj de la cara superior (con la operación U-1 ). La combinación resultante no será la misma que si simplemente se hubiera llevado a cabo la operación F, o sea girar la cara frontal 90 grados en sentido de las manecillas del reloj (quien no tenga un cubo Rubik a la mano, puede llevar a cabo esta operación usando alguno de los simuladores de los movimientos del cubo Rubik en sus computadoras de escritorio caseras). Para comodidad de quienes no tengan un cubo de Rubik a la mano, a continuación se llevarán a cabo estas operaciones utilizando el prorama Rubik.exe descrito anteriormente, con el cual partiendo de un cubo de Rubik en su configuración inicial:
le podemos aplicar una rotación de 90 grados en sentido de las manecillas del reloj a la cara superior (operación U) con el botón Ucw (Up clockwise). A continuación tenemos el aspecto que presenta el cubo al momento de estarse llevando a cabo esta operación:
Tras esto, podemos aplicar una rotación de 90 grados en sentido de las manecillas del reloj a la cara frontal (operación F) con el botón Fcw (Front clockwise). A continuación tenemos el aspecto que presenta el cubo al momento de estarse llevando a cabo esta operación:
Por último, aplicamos una rotación de 90 grados en sentido contrario de las manecillas del reloj a la cara superior (operación U-1) con el botón Uccw (Up counter-clockwise). A continuación tenemos el aspecto que presenta el cubo al momento en que se está terminando de llevar a cabo esta operación:
Ahora veamos lo que tendríamos si, partiendo de la configuración inicial de este cubo, le hubiésemos aplicado únicamente la operación F, una rotación de 90 grados en sentido de las manecillas del reloj de la cara frontal:
De este modo, el cubo de Rubik tal vez sea uno de los mejores maestros prácticos en la teoría de grupos que estudiante alguno pueda encontrar (sin demérito para muchos excelentes maestros universitarios que frecuentemente batallan para encontrar ejemplos ilustrativos que permitan al estudiante aprender y comprender el verdadero espíritu que está detrás de los conceptos abstractos que se le están enseñando).
Las enseñanzas del cubo de Rubik van mucho más lejos de lo que aquí se ha bosquejado. El notable matemático y profesor de ingeniería eléctrica Solomon W. Golomb (ampliamente conocido por ser el inventor del famoso juego polyomino que sirvió a su vez de inspiración para el juego Tetris, además de demostrar poseer un cociente intelectual IQ de 176 en el examen Mega IQ Power que originalmente apareció en la revista Omni) ha hecho hincapié en el hecho de que muchas partículas elementales de la física subatómica (como los quarks, los baryones y los anti-baryones) tienen su contraparte precisamente en el cubo de Rubik 3x3x3, lo cual sobresale al establecer los isomorfismos matemáticos entre los subgrupos del cubo de Rubik y las grupos de los cuales forman parte estas partículas. ¿Es esto algo meramente accidental, o tiene significancia de enorme importancia para los desarrollos posteriores que pueda tener la física en los años que habrán de venir?
==================
Pons Asinorum:
F2 B2 R2 L2 U2 D2