Grupos numéricos

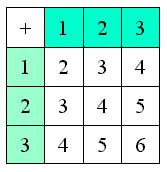
Aunque las matemáticas de la simetría son en su aplicación más general matemáticas sin números, ello no significa que no existan grupos cuyos elementos sean números. Sin embargo, construír un grupo usando números en donde la operación binaria (_°) sea una de las operaciones usuales de la aritmética como la suma (+) o la multiplicación (•) no es un asunto fácil, tomando en cuenta los requisitos de que debe existir un elemento identidad dentro del grupo, de que todo elemento debe tener un inverso, y de que la operación binaria no debe producir ningún elemento que esté fuera del grupo. Considérese por ejemplo el conjunto de números {1, 2, 3} bajo la operación de suma. Su tabla será:

Aunque el número “1” forma parte del conjunto, éste no nos sirve como elemento identidad, porque al actuar inclusive sobre sí mismo no produce el mismo elemento. Peor aún, se generan tres elementos, los números {4, 5, 6} que no forman parte del conjunto original de números; el conjunto no está cerrado bajo la adición. Y peor aún, no existe inverso alguno para ninguno de los números que forman parte del conjunto. Definitivamente, esto ni remotamente llena las expectativas de un grupo.

Considérese ahora el mismo conjunto de elementos bajo la operación de multiplicación. Su tabla será:

Tampoco en este caso tenemos algo que se parezca remotamente a un grupo. Aunque sí existe el elemento identidad, que en este caso es el número “1”, cuya operación binaria con cualquiera de los otros elementos nos produce el mismo número, no existen elementos inversos para los demás números del conjunto; no existe un elemento que multiplicado por el número “2” nos produzca el elemento identidad “1”, como tampoco existe un elemento que multiplicado por el número "3" nos produzca el elemento identidad. Y por si esto fuera poco, se generan tres números {4, 6, 9} que no forman parte del conjunto original, razón por la cual no hay cerradura.

Lo anterior nos puede dejar con la impresión de que no es posible construír un grupo a partir de los números cardinales que forman parte de la aritmética elemental.

Sin embargo, sí existen conjuntos de números que sí forman un grupo. Uno de ellos, el más sencillo de todos, es el conjunto {1, -1}, bajo la operación de multiplicación:

La única manera en la cual podemos construír grupos finitos usando números bajo operaciones usuales tales como la suma o la multiplicación es recurriendo al “aritmética de reloj” o aritmética modular. Recordemos primero lo que ocurre en la carátula de cualquier reloj conforme empieza a contar desde cero:

El conteo procede en forma ascendente pasando por 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, y 12; tras lo cual ya no hay un número como el 13 ó el 14 ó el 15 sino que la cuenta empieza nuevamente a partir de cero. Esto impide que la numeración se vaya acumulando en forma creciente hasta el infinito.

Esta forma de medir el tiempo que hoy nos puede parecer una gran idea de hecho fue concebida desde los tiempos de los Babilonios, para la cual dividieron el tiempo en 12 horas para cronometrar la mitad de un día. Sin embargo, no hay nada especial en la selección del número 12 como punto límite de conteo, los Babilonios podrían haber utilizado cualquier otro número como el número 10, el cual es más afín a nuestro sistema decimal. Si hubieran hecho tal cosa, los relojes de pared habrían tenido el siguiente aspecto:

Esta aritmética de reloj es lo que en matemáticas recibe el nombre más sofisticado (que quiere decir lo mismo) de aritmética modular. Para el manejo simbólico de la aritmética modular, utilizamos la siguiente definición:

a ≡ bmod(n)

que leemos de la siguiente manera:

“a es congruente a b módulo n”

y cuyo significado llano es:

“La diferencia a-b es dividida exactamente por n (sin dejar residuo)”

Bajo esta definición, el último reloj sería un reloj descrito por una aritmética modular módulo-10. El número n es el número límite en la aritmética modular después del cual el conteo comienza nuevamente a partir de cero. Con un reloj de pared basado en la división de la mitad de un día en 12 horas en mente, veamos cómo representaríamos en un conteo ascendente varias de las horas dadas por dicho reloj, comenzando por las dos de la mañana, seguido por las cinco de la mañana, y así sucesivamente:

2≡2mod(12)

5≡5mod(12)

7≡7mod(12)

11≡11mod(12)

13=1mod(12)

15=3mod(12)

20≡8mod(12)

Obsérvese que al llegar al número 13 dicho número 13 es convertido por la aritmética modular en el número 1, con lo cual el conteo comienza de nuevo. Del mismo modo, al llegar la manecilla principal del reloj (la que marca la hora) a lo que vendría siendo la quinceava posición, la aritmética modular convierte el número 15 en el número 3, con lo cual estaríamos leyendo “las 3:00 P.M. o tres de la tarde” (de cualquier manera, es importante tomar nota que la medición del tiempo también se acostumbra llevar a cabo en muchas partes dividiendo un día completo en 24 horas; sin embargo después de la “hora” 24 el conteo empieza otra vez desde cero, por lo cual también seguimos teniendo una aritmética de reloj, en este caso una aritmética módulo-24.) Bajo la aritmética modular, una suma módulo-12. jamás excederá dicho número 12, razón por la cual tenemos las siguientes relaciones modulares:

5+7≡12mod(12)

5+8≡1mod(12)

7+11≡6mod(12)

Con la aritmética modular, podemos tener una aritmética finita, con un conjunto finito de elementos que pueden formar un grupo.



Pero la artimética modular no sólo nos permite construír grupos mediante la operación binaria de adición; también nos permite construír grupos bajo la operación binaria de multiplicación numérica. Para ello, no es necesario agregar nuevos conceptos, todo lo que basta es aplicar el “reajuste” cuando el resultado de una multiplicación excede el módulo de la aritmética. Es así como tenemos lo siguiente bajo una aritmética módulo-12:

2x2≡4mod(12)

3x3≡9mod(12)

4x3≡12mod(12)

5x4≡8mod(12)

6x5≡6mod(12)