Matemáticas de la simetría

miércoles, 14 de diciembre de 2011

Indice

1. Un problema clásico del álgebra

2. Matemáticas sin números

3. Los grupos cíclicos

4. Subgrupos

5. Grupos numéricos

6. Los grupos de permutación

7. Los trasladados (cosets)

8. Los subgrupos normales

9. Las series de composición

10. El cubo de Rubik

11. Los grupos Galois

12. La imposibilidad de una fórmula quíntica

13. El producto de dos grupos

14. Generadores de grupos. Grafos de Cayley

15. Desarrollos posteriores

Un problema clásico del álgebra

Cuando un estudiante de enseñanza media tiene su primer contacto con el álgebra, generalmente es expuesto a un problema sencillo como el siguiente:

"Encontrar un número tal que si lo multiplicamos por cinco y le sumamos veinte nos dá treinta".

El número, desconocido aún, es identificado con la variable de incógnita x, con lo cual el problema es enunciado simbólicamente de la siguiente manera:

5x + 20 = 30

Aunque este problema es sencillo y se puede resolver mentalmente, muchos otros problemas que se ven posteriormente en los estudios del álgebra no lo son, razón por la cual se enuncia un problema introductorio de este tipo con fines didácticos.

La ecuación algebraica que tenemos arriba es lo que se llama una ecuación de primer grado, porque la incógnita x está elevada a un exponente de uno (1) en la ecuación. En su formulación más general, usando símbolos para representar los coeficientes numéricos, generalmente se representa de la siguiente manera;

ax + b = 0

La solución de este tipo de ecuaciones era ya conocida desde tiempos que predatan a la era Cristiana. La fórmula general para resolver una ecuación de primer grado como la de arriba es:

x = -b/a

Obsérvese que, si se conocen los coeficientes, la aplicación de la fórmula requiere que se lleve a cabo únicamente una división de los coeficientes.

El siguiente paso en la escala ascendente de complejidad es la ecuación de segundo grado, una ecuación que se enuncia en un problema de una manera como la siguiente:

"Dada la siguiente ecuacion

x² + 15x - 8 = 0

encontrar los valores de x para los cuales se cumple la ecuación."

La ecuación algebraica que tenemos arriba es lo que se llama una ecuación de segundo grado o ecuación cuadrática, porque la incógnita está elevada a un exponente máximo de dos (2) en la ecuación. Las soluciones a la ecuación cuadrática, no mediante alguna fórmula sino mediante manipulaciones geométricas (el álgebra aún no se había inventado) ya eran del conocimiento de los Babilonios unos 1,700 años A.C. Los textos de los Babilonios indican que ellos sabían resolver ecuaciones cuadráticas usando una "receta de cocina" concebida por algún genio matemático de la época mediante la cual se reformulaba el problema de modo tal que dijera: encontrar dos números, dados su suma y su producto. Llamando a los números s y p, y suponiendo que x+y=s y xy=p, la "receta de cocina" (o, en nuestra terminología moderna, el algoritmo de solución) era la siguiente:

(1) Tomar la mitad de s.

(2) Elevar al cuadrado el resultado.

(3) De lo que se obtenga, substraer p.

(4) Sacar la raíz cuadrada del resultado.

(5) Sumar esto a la mitad de s para obtener una de las soluciones. La otra es s menos este número.

Por ejemplo, si la suma es 8 y el producto es 15, entonces los pasos sucesivos dan 4, 16, 1, 1, 3 y 8-3=5. Así, los dos números buscados son 5 y 3.

Posterioremente, las ecuaciones de segundo grado fueron estudiadas de modo más sistemático por el matemático al-Khawarizmi (780-850 D.C.), de cuyo nombre deriva precisamente la palabra algoritmo (el procedimiento para resolver un problema mediante una secuencia ordenada de pasos siguiendo una "receta de cocina") y de cuya obra al-Jabr deriva la palabra álgebra. Es de notar que el manejo del tema dado por al-Khawarizmi a las ecuaciones cuadráticas es un asunto algo pesado en virtud de que sus proposiciones y demostraciones eran enunciadas usando palabras sin recurrir a símbolos algebraicos (los cuales aún no habían sido inventados ni siquiera por él), además de que todos sus argumentos son expuestos recurriendo a la geometría.

En la formulación más general de la ecuación cuadrática, usando símbolos para representar los coeficientes numéricos, generalmente se representa de la siguiente manera;

ax² + bx + c = 0

La fórmula general para resolver una ecuación de segundo grado cuando se conocen los coeficientes a, b y c, es la siguiente:

Es importante observar que la solución a la ecuación cuadrática general requiere la extracción de la raíz cuadrada de una función de los coeficientes conocida como el discriminante, b²-4ac. La derivación de esta fórmula se muestra a continuación:

Resueltas mediante fórmulas las ecuaciones de primer grado y segundo grado, el siguiente paso lógico en la escala de complejidad era la resolución también mediante alguna fórmula o fórmulas de las ecuaciones cúbicas o de tercer grado, generalmente expresadas de la siguiente manera:

ax³ + bx² + cx + d = 0

Pese a su deceptiva sencillez, el problema de resolver esta ecuación fue un reto muy duro por largo tiempo para los algebristas más diestros en los tiempos del Renacimiento. Las fórmulas para la resolución exacta de la ecuación cúbica general fueron publicadas en 1545 por Girolamo Cardano (1501-1576) en su libro Ars Magna. Además de la solución algebraica de las ecuaciones cúbicas, Cardano publicó en su Ars Magna una fórmula general para la solución de ecuaciones de cuarto grado:

ax⁴ + bx³ + cx² + dx + e = 0

como la siguiente:

x⁴ - 8x + 6 = 9

La resolución de la ecuación cúbica general mediante el uso de fórmulas tiene una historia interesante con acusaciones de plagio que involucran a Niccolò Fontana (1500-1557), mejor conocido como "Tartaglia" ("el Tartamudo"), uno de los mejores matemáticos de la época del Renacimiento. De acuerdo con la historia, Tartagila fue el primero en obtener fórmulas para la resolución de la ecuación cúbica general. Cuando se enteró de ello, Cardano convenció a Tartaglia de que le revelara su secreto para resolver las ecuaciones cúbicas bajo la promesa de que el secreto sería conservado siempre, aunque de cualquier manera el procedimiento de solución fue publicado el el Ars Magna por Cardano quien argumentó haber obtenido la solución cúbica de otra persona con la cual no estaba comprometido en pacto de confidencialidad. Es por esto que la solución mediante fórmulas de la ecuación cúbica es conocida hoy como el método Tartagia-Cardano, ya que aunque haya sido Tartaglia quien descubrió dichas fórmulas por vez primera, fue Cardano quien las dió a conocer al mundo entero al publicarlas en su libro. Y en cuanto a la resolución de la ecuación general de cuarto grado mediante el uso de fórmulas, esta fue lograda por un estudiante de Cardano, Ludovico Ferrari, la que fue incluída en el Ars Magna como el pináculo del álgebra tradicional.

Se agregará aquí que la solución Tartaglia-Cardano mediante fórmulas generales aplicadas a los coeficientes de una ecuación cúbica requiere la extracción de raíces cúbicas. Y en lo que respecta a la solución general a la ecuación general de cuarto grado lograda porLudovico Ferrari, esta requiere la extracción de raíces cuartas.

Si las soluciones de una ecuación pueden ser obtenidas a partir de sus coeficientes mediante las operaciones usuales de la aritmética (suma, resta, multiplicación y división) y la extracción de raíces (cuadradas, cúbicas, cuartas, etc.), por una larga costumbre histórica se dice que la ecuación es soluble por radicales.

Resueltas mediante fórmulas las ecuaciones de primero, segundo, tercero y cuarto grado, el siguiente paso lógico en la escala de complejidad era la búsqueda de alguna fórmula o fórmulas para resolver de la ecuación general de quinto grado o ecuación quíntica:

ax⁵ + bx⁴ + cx³ + dx² + ex + f = 0

Para lograr la solución de la ecuación general de quinto grado, las diversas técnicas usadas para la solución de ecuaciones de tercero y cuarto grado fueron sistematizadas en los tiempos de Cardano para que pudieran ser aplicadas a las ecuaciones de quinto grado. Pero aquí los mejores matemáticos de la época se toparon con enormes dificultades, dificultades que eclipsaban incluso los problemas que se tuvieron que enfrentar para la resolución de la ecuación cúbica. Y el problema no parecía ser uno de simple complejidad. Por alguna razón hasta entonces desconocida, la ecuación de quinto grado resistía tenazmente todo tipo de intentos para obtener una fórmula general o una serie de fórmulas generales para la resolución de dicha ecuación, entendiéndose por esto una fórmula maestra que proporcionase las soluciones recurriendo únicamente a las operaciones usuales de suma, resta, multiplicación, división y extracción de raíces (cuadradas, cúbicas, etc.) llevadas a cabo sobre los coeficientes de la ecuación.

Después de 300 años de búsquedas infructuosas, los matemáticos empezaron a sospechar que tales formulas no existían. Pero esto era tan solo una sospecha que podía ser descartada si mediante algún procedimiento ingenioso alguien lograba descubrir esas fórmulas que se resistían a ser descubiertas. Y precisamente en una época en la que la geometría de Euclides empezaría a desmoronarse de su pedestal como la única geometría posible (mis lectores pueden consultar aquí mi bitácora "Geometrías no-Euclideanas"), un joven matemático francés logró resolver el problema, y en el camino para la resolución del problema inventó un campo nuevo de las matemáticas, inventó las matemáticas de la simetría, inventó la teoría de grupos, la cual a la larga tendría una aplicación mucho más extensa que la resolución de este problema clásico del álgebra.

Matemáticas sin números

Quienes han estado acostumbrados toda su vida a usar números para todo desde que aprendieron en la escuela primaria a sumar, restar, multiplicar y dividir, tal vez les asombre saber que esta no es la única "aritmética" posible. Hay otros tipos de operaciones matemáticas que no usan números. Aquí comenzaremos la introducción a una de ellas. Aprenderemos el lenguaje de la simetría.

Por principio de cuentas, tenemos que definir una notación para nuestra nueva matemática sin números. Para ello, considérese algo que no puede ser representado con número alguno. Considérense las "operaciones" de ponerse los calcetines y ponerse los zapatos. Representemos cada una de ellas de la siguiente manera:

P = Ponerse los calcetines

Q = Ponerse los zapatos

Podemos hacer una combinación de estas operaciones, conviniendo para ello que una cadena sucesiva de operaciones se vaya escribiendo de izquierda a derecha. Puestos de acuerdo en esto, la operación binaria (llamada así porque combina a dos elementos) combinada

P ○Q

se debe interpretar como "ponerse los calcetines primero, y ponerse los zapatos después" (el símbolo ○ se puede leer simplemente como "operación", con lo cual lo anterior se leería simbólicamente como "P operación Q"). Obsérvese que la siguiente operación:

Q ○ P

es una operación absurda, ilógica, porque implica ponerse primero los zapatos y después los calcetines. Esto demuestra una cosa: Las operaciones dentro de nuestra nueva matemática no es necesariamente conmutativa. Hay muchos casos en los que pueden serlo, pero este no es uno de ellos.

Para cada operación, siempre debe ser posible definir una operación inversa. Así como nos podemos poner los calcetines (P) también nos los podemos quitar. Representaremos esta operación inversa de la siguiente manera:

P ^-1

con un "exponente" de -1. Es importante aclarar desde el principio que esto no tiene absolutamente nada que ver con el mismo exponente utilizado en el álgebra tradicional, que para un número a, representa simplemente su recíproco:

a ^-1 = 1/a

Nuestra notación de aquí en adelante para un inverso es puramente simbólica, sin ninguna operación "aritmética" posterior interna implicada. De este modo, la siguiente secuencia de operaciones:

Q^-1○ Q ○ P

nos producirá simplemente el siguiente efecto:

Aquí vemos que el efecto combinado de la operación:

Q^-1○Q

es dejar las cosas como están. Es una operación identidad, en forma similar a como actúa el número uno en la aritmética tradicional para la operación de multiplicación, en donde cualquier número multiplicado por el número uno nos produce el mismo número. Esta operación la representaremos con el símbolo I. El símbolo "I" que es la letra latina "i" mayúscula es utilizado en parte porque es la primera letra de la palabra "identidad", en parte porque se parece mucho al número uno con el cual comparte muchas propiedades, y en parte porque el uso de la letra "i" minúscula generalmente ya está reservado para representar la raíz cuadrada de -1, el símbolo de los números imaginarios, con lo cual el uso de la letra "i" para representar también al elemento identidad podría prestarse a confusiones cuando se manejan grupos en los que el número imaginario i es introducido como parte de los elementos de dichos grupos. (En muchos libros de texto, en lugar de usarse la letra I se utiliza la letra E mayúscula o la letra e minúscula, tomada de la primera letra de la palabra alemana Einheit que se traduce al español como "la unidad", siguiendo una costumbre de nomenclatura dejada por el físico-matemático Eugene Wigner.)

Obsérvese que las siguiente operaciones no están definidas:

P○ P y Q○ Q

Pero esto se debe a que no son operaciones de simetría propiamente dichas.

A continuación consideraremos una operación de simetría, la más sencilla de todas. En ella, tomamos una recta AB, y la hacemos girar en el plano de modo tal que el punto A sea movido a la posición que ocupaba el punto B y el punto B sea movido a la posición que ocupaba el punto A, como se muestra a continuación:

Esta es una operación de simetría auténtica, porque si borramos las letras, no tendremos forma alguna de distinguir la línea de la izquierda de la línea de la derecha.

Obsérvese aquí que hemos identificado dos operaciones básicas: la operación I, la operación identidad, que dejará a la línea tal y como estaba, y la operación r, una operación de rotación que cambiará los puntos extremos de la línea.

Así como en la aritmética tradicional podemos representar el producto de dos números cualesquiera con una tabla de multiplicar, aquí también podemos usar el equivalente de una "tabla de multiplicar". Pero tenemos que ser muy cuidadosos en cómo interpretaremos dicha tabla, porque si bien en una multiplicación el orden de los factores no altera el producto (es lo mismo poner 5*3 que 3*5), ya hemos asentado que aquí el orden de las operaciones tendrá un efecto muy importante sobre el resultado final.

Convendremos en que, para nuestra "tabla de multiplicación" como la que se muestra a continuación, la operación puesta en la columna extrema izquierda es la operación que se efectúa primero, mientras que la operación puesta en el renglón superior es la operación que se efectúa después:

De este modo, para la tabla mostrada, la entrada que corresponde al renglón p y a la columna q es:

p_{_°}q

que significa según lo que ya habíamos convenido "primero p y después q" o bien "p seguido de q". Trataremos de mantener este orden con el fin de concordar con la mayoría de la literatura matemática actual. Este tipo de "tabla de multiplicar" es también conocida como tabla Cayley, en honor al matemático inglés Arthur Cayley (1821-1895) quien fue quien la introdujo por vez primera en un trabajo suyo publicado en 1854 bajo el título "On the theory of groups". Como la definió por vez primera, el elemento identidad es escrito siempre correspondiendo al primer renglón y a la primera columna, costumbre que se sigue hasta nuestros días.

Regresando a la recta AB, la "tabla de multiplicar" que describe sus operaciones de simetría es la siguiente:

Obsérvese de la "tabla de multiplicación" que si aplicamos la operación r dos veces sucesivas, lo cual podemos representar simbólicamente como:

r² = r_{_°} r

regresamos la línea a su posición original. Esto significa que:

r² = I

O, viéndolo de otra manera, r es su propio inverso.

Veamos ahora otra serie de operaciones, para un triángulo equilátero, sobre el cual con sólo girar la hoja sobre la cual está trazado podemos llevar a cabo las siguientes operaciones de simetría:

En la primera operación, la operación P, tomamos el triángulo equilátero y lo hacemos girar en sentido contrario a las manecillas del reloj un ángulo de 120 grados. En la segunda operación, la operación Q, tomamos el triángulo equilátero y lo hacemos girar en sentido contrario a las manecillas del relos un ángulo de 240 grados. Las operaciones posibles se pueden representar mediante una "tabla de multiplicar" como la siguiente:

Ahora bien, si representamos al triángulo equilátero en su posición original con las letras ordenadas ABC, y si lo representamos habiendo girado de su posición original un ángulo de 120 grados con las letras CAB, y si lo representamos habiendo girado de su posición original un ángulo de 240 grados con las letras BCA, entonces podemos representar el efecto de aplicar las operaciones P y Q sobre dicho triángulo de la siguiente manera:

P(ABC) = CAB

P(CAB) = BCA

P(BCA) = ABC

Q(ABC) = BCA

Q(CAB) = ABC

Q(BCA) = CAB

De este modo, una sucesión de operaciones (recuérdese en todo momento que las operaciones que se van aplicando se van leyendo de izquierda a derecha) se puede representar como sigue:

Q○ P(ABC) = P○ (Q(ABC)) = P○ (BCA) = ABC

con lo cual podemos efectuar manipulaciones simbólicas más elaboradas sin necesidad de tener que recurrir a dibujo alguno como la siguiente:

P ○ Q ○ Q(CAB) =Q ○ Q(P(CAB)) = Q_{_°}Q(BCA)

= Q(Q(BCA)) = Q(CAB)

= ABC

En estos ejemplos, al ir aplicando una cadena sucesiva de operaciones, cada "operador" de rotación que actúa de inmediato sobre el objeto (el triángulo) es el que está escrito más hacia la izquierda.

Ahora vamos a ver el efecto de "romper" un poco la simetría de la figura. Tomemos el triángulo equilátero elevando su vértice A hacia arriba de modo tal que ya no sea un triángulo equilátero con sus tres lados iguales, sino un triángulo isósceles. Obviamente, ya no es posible aplicar las operaciones P y Q, porque si hacemos tal cosa la figura resultante ya no se va a parecer en nada a la figura original. De hecho, la única operación que podemos aplicar sobre este triángulo que nos dará una configuración igual a la original es la rotación del triángulo de modo tal que el vértice A permanezca en su sitio pero que los vértices B y C resulten intercambiados. Es, en efecto, lo que vendría siendo el equivalente de la operación S aplicada sobre el triángulo equilátero. Aunque el triángulo isósceles a primera vista nos parece una figura tan "simétrica" como el triángulo equilátero, no lo es, y esta es la razón por la cual todas las operaciones de simetría que se pueden llevar a cabo con el triángulo equilátero quedan reducidas a una sola con el triángulo isósceles. De hecho, el triángulo isósceles no tiene más operaciones posibles de simetría que las de la línea recta AB que vimos al principio.

La destrucción de la simetría en una figura reduce el número de operaciones de simetría que podemos llevar a cabo sobre ella. La cantidad posible de operaciones de simetría es una medida del grado de simetría que puede exhibir un objeto. Un objeto sin operación de simetría posible sobre él es un objeto completamente asimétrico.

Además de las operaciones de simetría P y Q arriba mostradas, podemos llevar a cabo otro tipo de operaciones sobre el triángulo equilátero, las cuales requieren girarlo manteniendo uno de sus vértices en el mismo lugar. Son las siguientes:

En la operación S, tomamos el triángulo equilátero y manteniendo el vértice superior fijo lo hacemos girar de modo tal que los vértices inferiores intercambien posiciones. En la siguiente operación T, mantenemos el vértice inferior izquierdo inmóvil y giramos el triángulo de modo tal que el vértice superior y el vértice inferior derecho intercambien posiciones. Por último, en la operación U, tomamos el triángulo equilátero y manteniendo el vértice inferior derecho inmóvil lo hacemos girar de modo tal que el vértice superior y el vértice inferior izquierdo intercambien posiciones. Las operaciones posibles aquí también se pueden representar mediante una "tabla de multiplicar" como la siguiente:

Los casos que hemos visto son casos de objetos geométricos localizables en un plano. Pero no hay razón alguna por la cual nos tenamos que limitar a objetos geométricos planos. Podemos extender nuestra matemática sin números hacia objetos sólidos, hacia un espacio de tres dimensiones.

La primera generalización que podemos hacer es sobre la recta AB que consideramos al principio. En lugar de una recta, podemos considerar el sistema de coordenadas rectangulares (x,y,z):

y podemos efectuar rotaciones de 180 grados en torno a cada uno de los ejes. Denotando como a, b y c a las rotaciones con respecto a los ejes x, y e z:

y denotando a I como la posición original, podemos construír la siguiente "tabla de multiplicación:

Siempre que construimos una "tabla de multiplicar" de este tipo encontraremos que cada elemento dentro de la tabla no puede aparecer más que una sola vez en un mismo renglón y en una misma columna; si aparece repetido entonces ello será el resultado de alguna equivocación en el cálculo del elemento.

El conjunto de elementos {I, a, b, c} que acabamos de ver caracterizado por la anterior "tabla de multiplicar" es un ejemplo de algo que en matemáticas es conocido como un un grupo, y en este caso este grupo es conocido como el 4-grupo de Klein. De hecho, todos los ejemplos anteriores en los que se han visto involucradas operaciones de simetría son ejemplos de grupos.

En todos los casos que hemos visto, las operaciones binarias entre dos elementos cualesquiera jamás producen un elemento que esté fuera del conjunto original de elementos. Para cada caso, el conjunto de elementos está cerrado, es completo y suficiente para poder llevar a cabo todas las operaciones. Esto es lo que llamamos la propiedad de cerradura. Podemos verificar también que en todos los casos se cumple la propiedad asociativa:

m _{_°} (n _{_°} o) = (m _{_°} n) _{_°} o

Por ejemplo, para el caso de la rotación de los ejes coordenados en ángulos de 180 grados, tenemos consultando la tabla que:

b _{_°} (c _{_°} a) = b _{_°} (c _{_°} a) = b _{_°} (b) = b _{_°} b = I

y que:

(b _{_°} c) _{_°} a = (a) _{_°} a = a _{_°} a = I

con lo que se concluye para esta combinación de operaciones que:

b _{_°} (c _{_°} a) = (b _{_°} c) _{_°} a

De aquí en adelante, todo conjunto de elementos (operaciones de simetría) en el que se ha definido una operación binaria (○) y en el que se cumplan las cuatro condiciones mencionadas, a saber:

(1) La operación binaria (○) jamás producirá un elemento que esté fuera del conjunto original de elementos. Siempre se cumplirá la propiedad de cerradura.

(2) Existe un elemento cuya aplicación "deja las cosas como están, el elemento identidad I.

(3) Toda operación puede ser cancelada en virtud de que dentro del conjunto de elementos cada operación tendrá un inverso que puede deshacer el efecto de la operación llevada a cabo.

(4) La propiedad asociativa se cumple en todos los casos. Los paréntesis no tienen efecto alguno sobre el resultado final de las operaciones y su uso está limitado a llevar a cabo operaciones de simplificación, no de fijación de algún orden en el cual se deban llevar a cabo las operaciones.

será llamado de aquí en adelante un grupo. Nuestro lenguaje matemático para estudiar la simetría de las cosas, será la teoría de grupos.

Puesto que es relativamente fácil en cualquier caso verificar la existencia del elemento identidad, así como confirmar con un vistazo rápido a la "tabla de multiplicar" que se cumple el requisito de que haya cerradura, así como verificar que todo elemento tiene su inverso, queda claro que lo más laborioso será verificar que la propiedad asociativa se cumple para todas las combinaciones posibles de tríos ordenados de elementos.

Aunque un grupo G que está asociado a una operación binaria "○" se representa frecuentemente como (G, ○), podemos prescindir de esta notación elaborada cuando no hay confusión alguna acerca del tipo de operación binaria que se lleva a cabo sobre los elementos del grupo.

En la teoría de los conjuntos, para un conjunto X como el siguiente:

X = {carlos, juan, pedro, lorenzo, javier}

denotamos como |X| la cantidad de elementos que contiene dicho conjunto. En este caso, |X|=5.

De la misma manera, por definición, el orden de un grupo G, representado como |G|, es la cantidad de elementos (operaciones de simetría) que contiene dicho grupo. Así, el 4-grupo de Klein {I, a, b, c} que vimos arriba tiene un orden de cuatro, o sea |G|=4. Del mismo modo, el grupo de operaciones de rotación {I, P, Q} del triángulo equilátero tiene un orden de tres, o sea |G|=3.

La definición del orden de un grupo nunca debe ser confundida con la definición del orden de un elemento del grupo. Se dice que un elemento cualquiera x de un grupo G es de orden finito si existe algún exponente n para el cual Xⁿ sea igual al elemento identidad I. En el 4-grupo de Klein, por ejemplo, el elemento a es de orden dos, porque a²=I.

Los grupos cíclicos

Existen grupos que cuyas tablas son extremadamente fáciles de generar. Son grupos tan inocentemente triviales que hasta un pequeño de primaria puede entender cómo producir la tabla de multiplicar para cualquiera de ellos. Se trata de los grupos cíclicos, lo cuales se distinguen porque constan de un solo elemento. Llamaremos al elemento a. Puesto que las únicas operaciones posibles son aquellas en las cuales el elemento es “multiplicado” consigo mismo, identificaremos una operación repetida n veces con un símbolo superscrito “n” (aunque resulta tentador llamarlo “exponente”, no se hará aquí tal cosa porque el elemento a no necesariamente es un número como los que usamos en la aritmética de uso corriente sino que puede ser una operación como las operaciones de simetría que ya hemos visto anteriormente). Así, el símbolo de la operación sucesiva a*a*a... repetida n veces será aⁿ. Para que estos grupos no sean infinitos tenemos que tener alguna manera de poder “contener” los efectos de una multiplicación repetida varias veces, y esto lo hacemos especificando que, para cierto valor de “n”, el resultado será el elemento identidad I. Por ejemplo, si el número "n" para el cual el resultado será el elemento identidad es 6, entonces:

a ○ a ○ a = a³

a ○ a ○a ○ a = a⁴ a ○ a ○ a ○ a ○ a = a⁵

a ○ a ○ a ○ a ○ a ○ a = I

a ○ a ○ a ○ a ○ a ○ a ○ a = a

a ○ a ○ a ○ a ○ a ○ a ○ a ○ a = a²

Esto nos permite poder construír de inmediato la siguiente “tabla de multiplicar”:

Al igual que con los grupos anteriores a los cuales con cada “tabla de multiplicar” se les ha podido asociar un conjunto de operaciones de simetría, también aquí existe una forma de poder hacer corresponder esta “tabla” con operaciones de simetría llevadas a cabo sobre una figura geométrica. Esto lo podemos hacer sobre la tabla anterior representando varios puntos igualmente espaciados alrededor de una circunferencia (a 60 grados el uno del otro) como sigue:

En este caso, la operación a consiste en hacer girar el disco en sentido contrario de las manecillas del reloj un ángulo de 60 grados. Al hacer esto, el punto A pasa a ocupar la posición que ocupaba el punto B, el punto B pasa a ocupar la posición que ocupaba el punto C, y así sucesivamente, hasta que el punto F pasa a ocupar el sitio dejado vacante por el punto A.

Nuevamente, tomando en cuenta que a representa una operación, podemos trabajar de modo puramente simbólico en la forma como se muestra a continuación prescindiendo por completo de dibujos:

a(ABCDEF) = BCDEFA

a²(ABCDEF) = a ○ a(ABCDEF) = a(BCDEFA) =CDEFAB

Ciertamente, el uso de notación simbólica permite economizar espacio y presentar la información de manera más compacta, en un estilo más “profesional”, más al gusto de los requerimientos rigurosos para la presentación de trabajos en publicaciones matemáticas serias. Pero esto no significa que limitarse exclusivamente al uso de símbolos sea la mejor manera de aprender o de explicar una cosa. Cuando se está aprendiendo algo nuevo como esto por vez primera, el uso profuso de dibujos aunado el uso profuso de ejemplos ayuda a aclarar muchas dudas y a “despejar” el panorama. Una vez que los conceptos fundamentales han entrado en nuestras mentes, una vez que tenemos una idea clara de aquello acerca de lo cual se está hablando, entonces podemos prescindir por completo de cualquier tipo de dibujos o inclusive de cualquier tipo de ejemplo limitándonos al uso de simbología pura, pero sin olvidar jamás que cuando ideas y conceptos nuevos van a entrar en nuestra cabeza por vez primera hay que referirse a aquello a lo cual se están refiriendo los símbolos. Pretender aprender (o inclusive desarrollar algo nuevo) de manera puramente simbólica sin ninguna conexión con algo tangible es perderse la oportunidad de darse cuenta de lo que realmente está sucediendo detrás de toda aquella simbología.

La simetría “rotacional” de los grupos cíclicos los hace reminiscentes del símbolo puesto en la bandera de la isla céltica Isle of Man situada cerca de la Gran Bretaña:

Puesto que el exponente n tiene forzosamente que tener un valor finito para que la simetría “rotacional” de disco se pueda preservar, los grupos cíclicos siempre serán grupos finitos. Sin embargo, a mayores valores de n, el orden del grupo irá aumentando conforme va aumentando la “densidad” de puntos en el borde de la circunferencia. Se había mencionado que entre menor sea la simetría presentada por un objeto también serán menos los elementos que contenga el grupo de las simetrías correspondientes a dicho objeto, hasta que en ausencia de simetría alguna el objeto sólo contendrá el elemento identidad. Indirectamente, esto puede interpretarse como la confirmación de que, de todos los objetos geométricos planos, la circunferencia es el objeto más simétrico de todos.

Subgrupos

Muchos grupos están contenidos dentro de grupos mayores. El grupo de rotaciones del cuadrado forma parte del grupo de todas las simetrías del cuadrado. El grupo de rotaciones y el grupo de reflexiones del triángulo equilátero están contenidos dentro del grupo de todas las simetrías posibles del triángulo equilátero. Estos “sub” grupos no están limitados a las operaciones que surgen en las operaciones de simetría llevadas a cabo sobre figuras geométricas planas o sólidas, es algo que surge de forma natural dondequiera que haya algo relacionado con algún tipo de simetría.

Algunas veces, dentro de una "tabla de multiplicar", es posible detectar un "sub" grupo dentro del grupo principal. Considérese la siguiente tabla en la que se ha definido r³=I y en la que se ha destacado un bloque de elementos:

-- subgrupo 1

Los elementos que pertenecen a este bloque cumplen con todos los tres requisitos para que sea clasificado como un grupo. El elemento identidad I está allí, se puede comprobar que la propiedad asociativa se cumple para todas las combinaciones posibles de elementos, y cada uno de los elementos dentro del bloque tiene su inverso. Este elemento más pequeño dentro del grupo original es clasificado efectivamente como un subgrupo.

¿Hay algún otro subgrupo dentro de la tabla?

A primera vista, esto no parece así. Sin embargo, sí hay otro subgrupo dentro de la tabla, pero para destacarlo hay que destacar los elementos del otro subgrupo con otro color:

-- subgrupo 2

Esquemáticamente, podemos representar a un grupo G que contenga a dos o más subgrupos de la siguiente manera:

En este ejemplo, el grupo G contiene dos subgrupos A y B. Obsérvese que tanto el subgrupo A como el subgrupo B contienen necesariamente por lo menos un elemento en común: el elemento identidad I. Este elemento siempre es común tanto al grupo principal como a los subgrupos que contenga.

La generalización de la definición de un grupo hacia un subconjunto de sus elementos como subgrupo se puede enunciar como un

Teorema: Sea G un grupo y sea H un subconjunto de elementos de dicho grupo. Entonces H será un subgrupo de G si y solo si:

(1) Para dos elementos cualesquiera x y y del subgrupo, la operación binaria * producirá un elemento que también formará parte del subgrupo.

(2) El subgrupo posee el elemento identidad I.

(3) Dentro del subgrupo cada elemento tiene su inverso.

Obsérvese que en las tres condiciones necesarias para que un conjunto de operaciones (elementos) pueda ser clasificado como un subgrupo no es necesario especificar una cuarta condición requiriendo que se cumpla la propiedad asociativa, ya que si los elementos del conjunto H provienen todos ellos de un grupo G en el que se cumple dicha propiedad, entonces los elementos de H también la heredarán.

Para que lo anterior pueda ser admitido en una publicación científica reconocida, se requiere presentar lo mismo que se ha dicho arriba usando un lenguaje más formal, más compacto, cargado con más símbolos y con letras más rebuscadas, presentando un aspecto más profesional que al mismo tiempo sea más obscuro para los no-profesionales, de una manera como la siguiente:

No se espante nadie que con cosas como esta cueste mucho trabajo tratar de convencer a los jóvenes de hoy que prosigan con una carrera en las matemáticas.

El procedimiento para detectar subgrupos dentro de un grupo principal G puede convertirse en un asunto laborioso conforme va aumentando el número de elementos del grupo principal. Si tenemos un grupo tal como el grupo G={I,a,b,p,r,s,t,x,y} y tenemos su "tabla de multiplicar", entonces tenemos muchas combinaciones posibles de elementos que potencialmente podrían constituír subgrupos, tales como:

H = {I, a, b}

H = {I, p, r, s, t}

H = {I, x, y}

H = {I, a, b, p, r, s, t}

H = {I, a, b, x, y}

En todos estos casos, además de que cada subgrupo H debe ser un grupo "completo" en el sentido de que ninguna operación binaria debe generar elemento alguno que no forme parte del subgrupo H, cada elemento del subgrupo tiene que tener un inverso dentro del mismo con el cual produzca el elemento identidad I. La verificación del cumplimiento de la propiedad asociativa no es tan importante en virtud de que si todos los elementos de un subgrupo H provienen de un grupo G en el cual cumplen la propiedad asociativa, entonces los elementos del subgrupo también la deberán de cumplir. En la búsqueda de subgrupos dentro de un grupo G, frecuentemente ayuda conocer el origen del grupo. Por ejemplo, si se trata del grupo de simetrías del triángulo equilátero, entonces podemos sospechar de que este grupo contiene por lo menos dos subgrupos: el grupo de rotaciones con respecto al centro de simetría del triángulo equilátero, y el grupo de reflexiones del triángulo. Y si se trata de grupos más complicados, puede resultar útil el intentar establecer alguna correspondencia de dichos grupos con grupos propios de figuras geométricas planas o sólidas en las cuales podamos visualizar a dichos subgrupos. En otras ocasiones, bastará con inspeccionar cuidadosamente la “tabla de multiplicar” de un grupo para detectar uno o varios subgrupos dentro de la misma. Desafortunadamente, la detección de los subgrupos dentro de un grupo mayor por mera inspección visual es una herramienta que requiere algo de intuición, la cual va perdiendo su valor conforme el tamaño de la tabla va aumentando. Para tablas muy grandes, no queda más remedio que recurrir a una computadora y utilizando un lenguaje simbólico darle a la computadora la tarea de encontrar todos los subgrupos que pueda haber dentro de un grupo mayor, lo cual puede ser una tarea intensiva en tiempo de cómputo hasta para una supercomputadora poderosa. Aunque resulta decepcionante el tener que confiar en una computadora para lograr la confirmación de un resultado importante o la demostración de un teorema, hay que aceptar esto como un hecho inevitable de la vida cuando la naturaleza del problema es tal que un humano haciéndolo todo sin el auxilio de una computadora requeriría de varias vidas para poder completar la tarea. Como motivo de interés histórico, se citará aquí que el primer teorema en ser demostrado por una computadora fue el concerniente a la famosa conjetura de los cuatro colores (bastan tan solo cuatro colores para poder pintar cualquier mapa sin que dos naciones compartan jamás una frontera con el mismo color), el cual fue resuelto por vez primera en 1976 por Kenneth Appel y Wolfgang Haken en la Universidad de Illinois. Esta demostración no es aceptada por muchos matemáticos hoy en día porque requiere tener fé en una máquina, en la infalibilidad de su compilador (el programa que convierte las instrucciones humanas en lenguaje de máquina) y el “hardware” que se está utilizando. Hasta la fecha, nadie ha podido presentar una prueba alterna que no requiera del uso de una máquina para poder llevar a cabo la demostración en un tiempo razonable.

Grupos numéricos

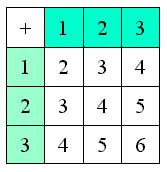
Aunque las matemáticas de la simetría son en su aplicación más general matemáticas sin números, ello no significa que no existan grupos cuyos elementos sean números. Sin embargo, construír un grupo usando números en donde la operación binaria (_{_°}) sea una de las operaciones usuales de la aritmética como la suma (+) o la multiplicación (•) no es un asunto fácil, tomando en cuenta los requisitos de que debe existir un elemento identidad dentro del grupo, de que todo elemento debe tener un inverso, y de que la operación binaria no debe producir ningún elemento que esté fuera del grupo. Considérese por ejemplo el conjunto de números {1, 2, 3} bajo la operación de suma. Su tabla será:

Aunque el número “1” forma parte del conjunto, éste no nos sirve como elemento identidad, porque al actuar inclusive sobre sí mismo no produce el mismo elemento. Peor aún, se generan tres elementos, los números {4, 5, 6} que no forman parte del conjunto original de números; el conjunto no está cerrado bajo la adición. Y peor aún, no existe inverso alguno para ninguno de los números que forman parte del conjunto. Definitivamente, esto ni remotamente llena las expectativas de un grupo.

Considérese ahora el mismo conjunto de elementos bajo la operación de multiplicación. Su tabla será:

Tampoco en este caso tenemos algo que se parezca remotamente a un grupo. Aunque sí existe el elemento identidad, que en este caso es el número “1”, cuya operación binaria con cualquiera de los otros elementos nos produce el mismo número, no existen elementos inversos para los demás números del conjunto; no existe un elemento que multiplicado por el número “2” nos produzca el elemento identidad “1”, como tampoco existe un elemento que multiplicado por el número "3" nos produzca el elemento identidad. Y por si esto fuera poco, se generan tres números {4, 6, 9} que no forman parte del conjunto original, razón por la cual no hay cerradura.

Lo anterior nos puede dejar con la impresión de que no es posible construír un grupo a partir de los números cardinales que forman parte de la aritmética elemental.

Sin embargo, sí existen conjuntos de números que sí forman un grupo. Uno de ellos, el más sencillo de todos, es el conjunto {1, -1}, bajo la operación de multiplicación:

La única manera en la cual podemos construír grupos finitos usando números bajo operaciones usuales tales como la suma o la multiplicación es recurriendo al “aritmética de reloj” o aritmética modular. Recordemos primero lo que ocurre en la carátula de cualquier reloj conforme empieza a contar desde cero:

El conteo procede en forma ascendente pasando por 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, y 12; tras lo cual ya no hay un número como el 13 ó el 14 ó el 15 sino que la cuenta empieza nuevamente a partir de cero. Esto impide que la numeración se vaya acumulando en forma creciente hasta el infinito.

Esta forma de medir el tiempo que hoy nos puede parecer una gran idea de hecho fue concebida desde los tiempos de los Babilonios, para la cual dividieron el tiempo en 12 horas para cronometrar la mitad de un día. Sin embargo, no hay nada especial en la selección del número 12 como punto límite de conteo, los Babilonios podrían haber utilizado cualquier otro número como el número 10, el cual es más afín a nuestro sistema decimal. Si hubieran hecho tal cosa, los relojes de pared habrían tenido el siguiente aspecto:

Esta aritmética de reloj es lo que en matemáticas recibe el nombre más sofisticado (que quiere decir lo mismo) de aritmética modular. Para el manejo simbólico de la aritmética modular, utilizamos la siguiente definición:

a ≡ bmod(n)

que leemos de la siguiente manera:

“a es congruente a b módulo n”

y cuyo significado llano es:

“La diferencia a-b es dividida exactamente por n (sin dejar residuo)”

Bajo esta definición, el último reloj sería un reloj descrito por una aritmética modular módulo-10. El número n es el número límite en la aritmética modular después del cual el conteo comienza nuevamente a partir de cero. Con un reloj de pared basado en la división de la mitad de un día en 12 horas en mente, veamos cómo representaríamos en un conteo ascendente varias de las horas dadas por dicho reloj, comenzando por las dos de la mañana, seguido por las cinco de la mañana, y así sucesivamente:

2≡2mod(12)

5≡5mod(12)

7≡7mod(12)

11≡11mod(12)

13=1mod(12)

15=3mod(12)

20≡8mod(12)

Obsérvese que al llegar al número 13 dicho número 13 es convertido por la aritmética modular en el número 1, con lo cual el conteo comienza de nuevo. Del mismo modo, al llegar la manecilla principal del reloj (la que marca la hora) a lo que vendría siendo la quinceava posición, la aritmética modular convierte el número 15 en el número 3, con lo cual estaríamos leyendo “las 3:00 P.M. o tres de la tarde” (de cualquier manera, es importante tomar nota que la medición del tiempo también se acostumbra llevar a cabo en muchas partes dividiendo un día completo en 24 horas; sin embargo después de la “hora” 24 el conteo empieza otra vez desde cero, por lo cual también seguimos teniendo una aritmética de reloj, en este caso una aritmética módulo-24.) Bajo la aritmética modular, una suma módulo-12. jamás excederá dicho número 12, razón por la cual tenemos las siguientes relaciones modulares:

5+7≡12mod(12)

5+8≡1mod(12)

7+11≡6mod(12)

Con la aritmética modular, podemos tener una aritmética finita, con un conjunto finito de elementos que pueden formar un grupo.

Pero la artimética modular no sólo nos permite construír grupos mediante la operación binaria de adición; también nos permite construír grupos bajo la operación binaria de multiplicación numérica. Para ello, no es necesario agregar nuevos conceptos, todo lo que basta es aplicar el “reajuste” cuando el resultado de una multiplicación excede el módulo de la aritmética. Es así como tenemos lo siguiente bajo una aritmética módulo-12:

2x2≡4mod(12)

3x3≡9mod(12)

4x3≡12mod(12)

5x4≡8mod(12)

6x5≡6mod(12)

Los grupos de permutación

Existen unos grupos extremadamente importantes en las matemáticas de la simetría, conocidos como los grupos de permutación.

Para empezar, supóngase que tenemos un arreglo inicial que consta de seis objetos acomodados en forma ordenada en sus casilleros respectivos, un arreglo en donde aún no se ha llevado a cabo ninguna permutación sobre dichos objetos. Esta configuración inicial, la cual identificaremos como la permutación identidad I, usualmente se representa en los textos de matemáticas de la siguiente manera:

Sin embargo, con la intención de dar una mayor claridad y amenidad a lo que estaremos estudiando aquí, se utilizará una representación equivalente complementada con varios colores que nos ayudarán a distinguir mejor cada movimiento que se estará llevando a cabo sobre los elementos individuales. De este modo, la anterior representación será manejada del modo siguiente:

enfatizándose que las dos representaciones son completamente equivalentes.

Ahora llevaremos a cabo una permutación de elementos, la cual identificaremos con el símbolo k. Todos los cambios los llevaremos a cabo en el renglón inferior, mientras que el renglón superior permanecerá inalterado. El elemento que está en la posición 1 será relocalizado a la posición 5, el elemento que está en la posición 2 se dejará en su mismo lugar, el elemento que está en la posición 3 será relocalizado a la posición 4, el elemento que está en la posición 1 será relocalizado a la posición 1, el elemento que está en la posición 5 será relocalizado a la posición 3, y el elemento que está en la posición 6 se dejará en su mismo lugar. Una vez que se han llevado a cabo estos movimientos, nuestro arreglo rectangular presentará el siguiente aspecto:

De este modo, bajo la operación k, cada uno de los elementos inferiores del arreglo han sido reasignados según el siguiente esquema:

k(1) → 4

k(2) → 2

k(3) → 5

k(4) → 3

k(5) → 1

k(6) → 6

Esta transformación es lo que en matemáticas se conoce como un mapeo (mapping), llamado también aplicación(en el sentido matemático de que se aplica una transformación al elemento convirtiéndolo en otro elemento). El término es apropiado, porque bajo una operación o transformación como k, cada elemento del conjunto original es mapeado hacia una nueva configuración.

Una vez que el concepto anterior ha quedado claro, podemos proceder a llevar a cabo una sucesión de permutaciones, o si queremos utilizar terminología más elegante, una composición. Para simplificar la explicación, lo haremos utilizando dos permutaciones sobre cinco elementos en lugar de seis, las cuales llamaremos h y d.

La permutación h la podemos representar de la siguiente manera:

Del mismo modo, la permutación d la podemos representar de la siguiente manera:

Ahora llevaremos a cabo la siguiente secuencia de permutaciones:

h ○ d

Para poder llevar a cabo esta secuencia combinada de permutaciones, podemos reacomodar las columnas de la permutación d de modo tal que el primer renglón de la permutación d coincida con el segundo renglón de la permutación h. De este modo, la permutación d:

quedará representada de la siguiente manera:

Este reacomodo de columnas es una operación completamente válida y siempre la podemos llevar a cabo, puesto que el orden de las columnas en cualquier permutación no tiene relevancia alguna, en el caso que nos ocupa ambos arreglos representan la misma aplicación:

d(1) → 1

d(2) → 5

d(3) → 3

d(4) → 4

d(5) → 2

De este modo, la operación binaria h ○ d representa ahora el siguiente aspecto:

Hecho esto, el último paso es inmediato. Podemos ver que las entradas del renglón inferior de la primera permutación h cancelan las entradas del renglón superior de la segunda permutación d, con lo cual tenemos la resultante final de esta composición de permutaciones:

A continuación, aplicaremos el mismo procedimiento para obtener la resultante de la operación combinada d ○ h:

Nuevamente, podemos llevar a cabo un reacomodo de las columnas en la segunda permutación, la permutación h, de modo tal que el primer renglón de la segunda permutación h coincida con el segundo renglón de la primera permutación d, llevando a cabo tras esto la cancelación de dichos renglones para obtener el efecto final de la permutación combinada:

o en notación convencional sin usar los adornos didácticos que hemos venido utilizando:

Como puede apreciarse, lo que obtenemos con la operación h ○ d no es igual a lo que obtenemos con la operación d ○ h. En general, la secuencia sucesiva de dos o más permutaciones no es una operación conmutativa.

Aunque el ejemplo anterior fue llevado a cabo sobre un conjunto de cinco elementos, el procedimiento se puede extender sin problema alguno hacia un conjunto mayor de elementos. A continuación tenemos otro ejemplo en el cual llevamos a cabo dos permutaciones sucesivas sobre un conjunto de seis elementos:

o en notación convencional:

Mediante la representación que hemos venido utilizando, es extremadamente fácil obtener la permutación inversa de una permutación dada. Dada una permutación cualesquiera m como la que se muestra a continuación, todo lo que tenemos que hacer para obtener la permutación inversa m^-¹ es intercambiar el renglón superior y el renglón inferior, y tras esto reacomodar las columnas de modo tal que los números del renglón superior tengan una secuencia de orden ascendente:

Llevando a cabo operaciones de composición binaria para permutaciones como las que vimos arriba, el lector pueden comprobar por cuenta propia lo siguiente:

m ○ m^-1 = I

m^-1 ○ m = I

Veamos ahora lo mismo pero desde otro punto de vista.

Existe otro tipo de notación matemática extremadamente útil para abreviar la representación de una permutación, una especie de notación matemática “taquigráfica” breve. Es la notación cíclica.

Supóngase que tenemos un tablero de ajedrez en el cual tenemos colocado un alfil en la posición 1, una torre en la posición 2, y un caballo en la posición 3. Supóngase ahora que llevamos a cabo una permutación en la cual movemos el alfil de la posición 1 a la posición 2, la torre de la posición 2 a la posición 3, y el caballo de la posición 3 a la posición 1 que había sido dejada vacante por el alfil. La siguiente figura muestra el reacomodo llevado a cabo sobre la configuración original:

Bajo el esquema conocido como notación cíclica, este reacomodo es simbolizado de la siguiente manera:

(1__2_{__}3)

y se lee de la siguiente manera:

“Muévase la pieza que estaba en la posición 1 a la posición 2; tras esto muévase la pieza que estaba en la posición 2 a la posición 3; y por último, muévase la pieza que estaba en la posición 3 al lugar indicado al inicio del ciclo, al lugar 1”

En general, la permutación básica

es llamada un ciclo de longitud n, y se representa como:

(a₁__a_{2__}a_{3__}a₄__a₅ ...... a_n)

lo cual quiere decir, leyendo de izquierda a derecha, que los elementos son reposicionados bajo el siguiente esquema:

a₁ → a₂

a₂ → a₃

a₂ → a₃

a₃ → a₄

a₄ → a₅

y así sucesivamente, terminando con el sobreentendido de que el elemento en la última posición, a_n, es asignado a la primera posición a₁, o sea:

a_n → a₁

De este modo:

Sin embargo, un ciclo puede actuar sobre una cantidad inferior de elementos. Por ejemplo, en el caso arriba citado, (1_2_4) se lee como:

o bien, "el elemento en la primera posición 1 es asignado a la posición 2, el elemento en la segunda posición 2 es asignado a la posición 4, y el elemento en la posición 4 es asignado a la posición 1". En virtud de que los elementos 3, 5 y 6 no cambian de posición, no aparecen mencionados dentro del ciclo.

Como la notación cíclica no nos dice cuántos elementos hay dentro del grupo de permutación al cual algún ciclo esté haciendo referencia, la notación (1_2_4) podría interpretarse de varias maneras, tales como:

Es por esto que resulta muchas veces conveniente complementar una notación cíclica indicando el grupo de permutación S_n al cual pertenece cierto elemento (ciclo). En los tres casos arriba mencionados, lo haríamos de la siguiente manera:

(1__2__4) ∈ S₄

(1__2__4) ∈ S₅

(1__2__4) ∈ S₆

Desafortunadamente, esta no es una práctica que se siga en todos los libros de texto. De cualquier manera, y afortunadamente, es posible saber dentro del contexto de los ejemplos citados en dichos textos cuál es el grupo de permutación S_n al que se está refiriendo cierta notación cíclica.

Obsérvese que el ciclo

(1__2__3)

también se puede escribir como

(3__1__2)

ya que en ambos casos se está proporcionando la misma información. Sin embargo, no es posible escribirlo como

(3__2__1)

Consideremos ahora los siguientes ciclos:

(1__2__4) ∈ S₆

(1__2__5__6) ∈ S₆

entonces un posible producto de estos ciclos:

(1__2__4) ○ (1__2__5__6)

será igual a:

Por otro lado, tenemos que:

Obsérvese que los dos resultados son diferentes. En general, el producto de dos ciclos no es conmutativo, aunque puede serlo bajo ciertas condiciones. Por ejemplo, considérense los siguientes ciclos:

(1__4) ∈ S₆

(2__3__5) ∈ S₆

Entonces las permutaciones combinadas:

(1__4) ○ (2__3__5)

(2__3__5) ○ (1__4)

producen el mismo resultado:

La diferencia entre este ejemplo y el ejemplo previo es que en tanto los ciclos (1_4) y (2_3_5) no tienen números en común, los ciclos (1_2_4) y (1_2_5_6) sí tienen números en común, el número 1 y el número 2. Para que el producto de dos ciclos sea conmutativo, se requiere que no tengan números en común. En general, se dice que los ciclos en una colección de productos de ciclos son disjuntos si no tienen números repetidos. Así, los ciclos (1_4_8_9) y (2_4_7_9) no son disjuntos (tienen los números 4 y 9 en común) y por lo tanto el producto de los mismos no será conmutativo, mientras que los ciclos (1_3_5_8) y (1_2_4) sí son disjuntos y por lo tanto sus productos serán conmutativos. Los ciclos disjuntos siempre son conmutativos porque operan en subconjuntos disjuntos del conjunto {1, 2, 3, 4, 5, ... , n}.

Ahora aprenderemos la manera de poder escribir una permutación como un producto de ciclos disjuntos. Considérese la siguiente permutación del grupo S₈:

Empezamos con el número 1 y le seguimos el rastro para ver qué sucede con el 1 y sus imágenes sucesivas. Vemos que:

1 → 2 → 4 → 1

así que empezamos escribiendo nuestro primer ciclo (1_2_4). Ahora tomamos el siguiente número que no haya sido utilizado, que en este caso es el 3, y le seguimos el rastro para ver qué sucede con el 3 y sus imágenes sucesivas. Encontramos que:

3 → 5 → 7 → 3

con lo cual escribimos nuestro segundo ciclo como (3_5_7). Nuevamente, tomamos el siguiente número que no haya sido utilizado, en este caso el 6, y le seguimos el rastro, encontrando que:

6 → 8 → 6

con lo cual se podemos escribir el último ciclo como (6_8). Agotados los números, podemos escribir en notación cíclica la permutación original como:

(1_2_4)(3_5_7)(6_8)

Este ejemplo puede ser generalizado con el siguiente

Teorema: Cualquier permutación con un conjunto finito de elementos siempre se puede escribir como un producto de ciclos disjuntos.

Sabiendo cómo representar permutaciones mediante la notación cíclica, podemos construír una “tabla de multiplicar” para resumir las operaciones combinadas dentro de un grupo de permutación que de otra manera no sería fácil de construír, el grupo simétrico de permutación S₃, en donde la letra “S” significa precisamente “simétrico” y el número 3 representa el número de objetos que generan al grupo, el cual consta de (3)(2)(1)=6 elementos en total (si nos referimos a este último dato como el orden del grupo para ser “elegantes”, escribiríamos |S3|=6), empezando con el elemento identidad que en notación cíclica se representa simplemente como (1):

(1)

(1_2_3)

(1_3_2)

(1_2)

(1_3)

(2_3)

Este es precisamente el grupo de permutación que describe todas las permutaciones posibles en las tres piezas (el alfil, la torre y el caballo) del ejemplo que vimos en nuestro tablero de ajedrez. La “tabla de multiplicación” será la siguiente:

Obsérvese que dentro de la “tabla de multiplicar” para el grupo de permutación S(3), también representado en la literatura como S₃, se ha destacado un subgrupo. Este es un subgrupo conocido como el grupo A(3) -también identificado frecuentemente como A₃- y es nuestro primer ejemplo de un grupo alternante de permutación, en donde la letra “A” significa precisamente “alternante” y el número que le sigue indica el número de elementos que generan a dicho grupo. Los grupos alternantes son aquellos que consisten únicamente de todas las permutaciones que llamamos pares, lo cual será el tema de estudio de la siguiente entrada.